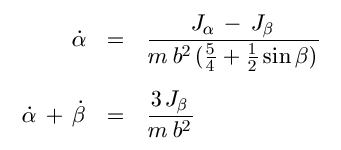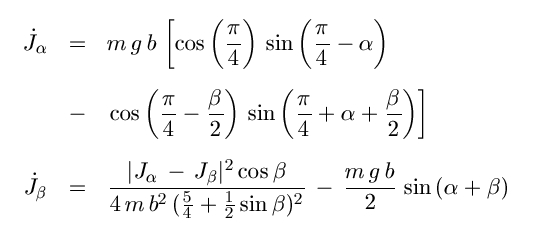Das Video:

Das Rottsche Pendel in Aktion

Schon immer war das mechanische Pendel ein Symbol für Harmonie und Ordnung in der Natur. Ein faszinierend einfaches mechanisches Instrument, das elementarsten physikalischen Prinzipien folgt und die Zeit mit größter Verläßlichkeit in immer gleiche Abschnitte einzuteilen vermag: Es bestimmt den Gang unserer Uhren und ist das irdische Gegenstück zu den Planeten und Gestirnen im Weltall, die durch ihre wiederkehrende Bahn Tage, Monate und Jahre definieren.

Der Gegensatz, den uns das hier abgebildete Rottsche Pendel demonstriert, könnte kaum schärfer sein. Es handelt sich um ein Pendel, an dessen Arm ein zweites Pendel aufgehängt ist. Durch diese geringe konstruktive Änderung wandelt sich sein Verhalten zu einem beunruhigenden Beweis der latenten Irregularität der Natur. Es kennt keine periodische Wiederkehr seiner Schwingungen, es gibt keine geschlossen lösbare mathematische Formel, die seine Bewegung über längere Zeiträume vollständig vorhersagen könnte.

Statt den Betrachter durch periodische Wiederhohlung der Pendelausschläge zu beruhigen, vollführt das Rottsche Pendel mit seinen beiden Hebeln wilde Tänze. Wie wahnsinnig rudert es bis zur Erschöpfung seiner Energie mit den Armen. Nie gelingt es, zweimal hintereinander den gleichen Bewegungsablauf herbeizuführen.

Für mein Wohnzimmer habe ich mir ein Rottsches Pendel gebaut. Ein Blickfang, der jeden Besucher in seinen Bann zieht. Damit das Pendel einwandfrei funktioniert und nicht schon nach wenigen Pendelschlägen wieder zum Stillstand kommt, ist bei der Fertigung eine gewisse mechanische Präzission unabdingbar: einerseits muß das Pendel genügend Masse haben, gleichzeitig müssen die beiden Gelenke leichtgängig sein. Das abgebildete Pendel wurde aus Eisenstäben von 25 mal 6 mm Querschnitt hergestellt, die ich aus Schrottteilen herausgesägt habe. Die drei Stücke für die beiden Pendelarme haben eine Länge von 18 cm. Das gesamte Pendel ist 31 cm hoch und muß mit einer Schraubzwinge am Wohnzimmerschrank befestigt werden, wenn es schwingt.

Das Pendel hat zwei Gelenke: eines in der Mitte des Querhebels, das zweite an seinem rechten Ende. Hier ist einer der beiden vertikalen Hebel gelagert. Der zweite vertikale Hebel ist im rechten Winkel fest am gegenüberliegenden Ende des Querhebels angelötet. Beide Lager müssen eine komplette Rundumbewegung der Hebel zulassen.

Wichtig ist eine genaue Passung der Lagerbolzen: ein polierter Stahlstift mit 4 mm Durchmesser, der in einer Messingbuchse läuft. Die Stahlstifte sind an den Hebeln festgelötet. Wichtig ist, dass das seitliche Spiel gering ist und die Hebel beim Umlauf nicht aneinanderstoßen. Auf den Stahlstift des mittleren Lagers habe ich einen Messingring aufgelötet, damit der Querhebel nicht von der Halterung herunterfallen kann. Das Lager am rechten Ende wird mit einer Lüsterklemme gesichert.

Ich habe darauf verzichtet, das Pendel zu lackieren, zumal die matte, mit einer groben Drahtbürste abgeriebene Oberfläche des Eisens sehr interessante Lichtreflexe ergibt. Damit das Pendel keinen Rost ansetzt, fette ich es gelegentlich leicht mit Nähmaschinenöl ein.

Hier geht es rund! Das Pendel verträgt auch den härtesten Betrieb. Da wackelt der zentnerschwere Wohnzimmerschrank und das Geschirr klappert. Die Nase sollte man nicht zu nah dranhalten, denn das Pendel ist unberechenbar ! Eine gute Justierung der Lager und ein stabil montierter Fuß sind wichtig, sonst wird die Bewegungsenergie des Pendels durch die Vibration auf den darunterstehenden Tisch oder Schrank übertragen.

Die schönsten Figuren zeigt das Pendel jedoch im mittleren Drehzahlbereich, wenn sich die Hebel gerade eben noch überschlagen. Dann gibt es immer wieder Richtungsänderungen - die Bewegungsenergie fließt zwischen den beiden Hebeln hin und her.

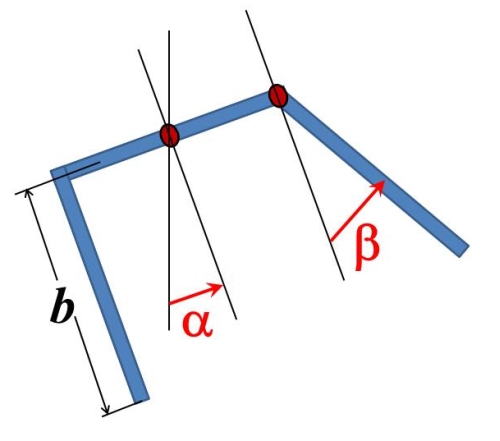
Das Schema des Pendels: drei Stäbe der Länge b und der Masse m, die an einem festen Knie und an zwei Drehlagern miteinander verbunden bzw. aufgehängt sind.

Hier klicken: der detaillierte Bericht zur Physik des Pendels zum Download

Für den mathematisch interessierten Besucher dieser Seite sei hier auch das System die vier gekoppelten Differentialgleichungen angegeben, dem das Pendel unter Vernachlässigung von Reibungsverlusten folgt. Hierbei faßt man die beiden Gelenkwinkel α und β (siehe Abb. links) sowie die Drehimpulse J_α und J_β der Massen um diese Gelenke als Funktion der Zeit auf. Ein Punkt über der jeweiligen Winkelgröße bedeutet die Zeitableitung. Ferner sind b die Länge eines jeden der drei Hebel, m deren Masse und g die Erdbeschleunigung. Das Gleichungssystem ist von erster Ordnung in der Zeit und läßt sich nummerisch sehr gut mit dem Runge-Kutta-Verfahren über eine gewisse Zeitspanne lösen. Eine geschlossene analytische Lösung existiert nicht.